<Java>14 树
本文最后更新于:2025年8月16日 凌晨
14 树
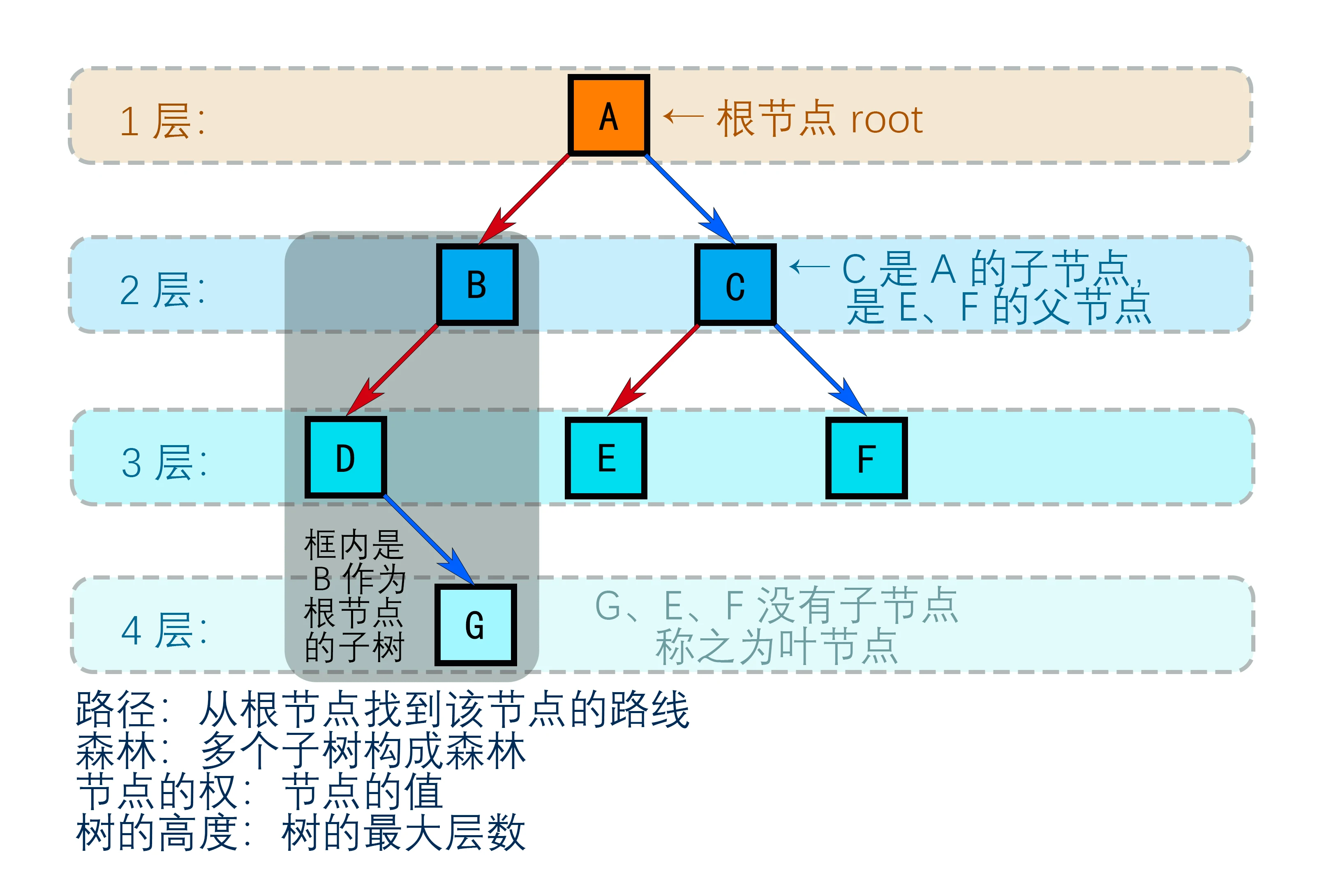
#什么是树?
| 结构严格派 有唯一的父节点 |
结构中立派 有前驱和后继关系就行 |
结构自由派 能存放大量数据就行 |
|
| 类型严格派 是一种非线性数据结构 |
红黑树是树 | 图也是树 | 哈希表也是树 |
| 类型中立派 是数据结构就行 |
链表也是树 | 队列肯定是树 | 数组也可以是树 |
| 类型自由派 和编程有关就行 |
类当然是树 | 接口也是树 | 文件也是树! |
14.1 二叉树:
(树结构图_14.1)
-
**二叉树:**树有多种。每个节点最多只能有 2 个子节点的一种树的形式称为二叉树
二叉树的子节点分为 左节点 和 右节点。
-
**满二叉树:**二叉树的 所有叶节点 都在 最后一层,且节点总数是 2n - 1
-
**完全二叉树:**二叉树的 所有叶节点 都在 最后一层 和 倒数第二层,且最后一层的叶节点在左侧连续、倒数第二层的叶节点在右侧连续
#二叉树的遍历:
-
**前序遍历:**先输出父节点,再遍历左子树和右子树。
自根节点起。先输出当前节点。再递归前序遍历左节点。那之后,递归前序遍历右节点。
public static class Node { // 节点类 int val; Node left; Node right; } public static String traverse(Node root) { StringBuilder sb = new StringBuilder(); traverse(root, sb); return sb.toString(); } private static void traverse(Node root, StringBuilder sb) { if (root == null) return; sb.append(root.val).append(" "); // 先输出父节点 traverse(root.left, sb); // 再遍历左子树 traverse(root.right, sb); // 再遍历右子树 } -
**中序遍历:**先遍历左子树,再输出父节点,再遍历右子树。
-
**后序遍历:**先遍历左子树,再遍历右子树,再输出父节点。
14.1.1 顺序存储二叉树
从数据存储来看,数组与树可以相互转换。数组可以转换成树,树也能转换成数组。
顺序存储二叉树通常只考虑完全二叉树。将数组转换成树后,将可以进行前序、中序、后序遍历。
顺序存储二叉树的例子:
int[] array = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10};该 array 的顺序存储二叉树为:
graph TD
A(0)---B(1)---C(3)
A---a(2)---aa(5)
B---D(4)
a---ab(6)
C---E(7)
C---F(8)
D---G(9)
D---H(10)#顺序存储二叉树的转换:
-
数组下标为 0 的元素放在根节点。
-
对于数组下标为 n 的元素,其左子节点的数组下标为 2 × n + 1、右子节点的数组下标为 2 × n + 2、父节点的数组下标为 (n - 1) / 2
可以发现,所有左节点都是奇数下标,右节点都是偶数下标
public static Node toTree(int[] array) {
Node root = new Node(array[0]);
List<Node> list = new ArrayList<Node>();
list.add(root); // 数组下标为 0 的元素放在根节点。
for (int i = 1; i < array.length; i++) { // 按照前述方法,创建每个元素节点,并放在对应父节点下
Node temp = new Node(array[i]);
list.add(temp);
Node parent = list.get((i - 1) / 2);
if (i % 2 == 0) parent.right = temp;
else parent.left = temp;
}
return root;
}
public static class Node {
public int val;
public Node left;
public Node right;
public Node(int val) {
this.val = val;
}
}以上是一种显式的转换。也可以直接将数组视为抽象的顺序存储二叉树。
如:堆。——见 [5.4.8 堆排序]
14.1.2 线索化二叉树
含有 n 各节点的二叉链表中,有 n + 1 个空指针域。利用这些空指针域,存放指向节点在某种遍历次序下的前驱和后继节点的指针,这种附加的指针称为 线索。加上了线索的二叉链表称为 线索链表,相应二叉树称为 线索二叉树。
线索二叉树可分为:前序线索二叉树、中序线索二叉树、后续线索二叉树。
线索化二叉树后,那些左节点和右节点既可能指向 自身的子树,也可能指向自身的 前驱 / 后继 节点。因此,需要添加一组标记,以记录线索的种类。
这个遍历的场合,不能再使用递归方式遍历,而是改为线性方式遍历即可。
14.1.3 赫夫曼树
给定 n 个权值作为 n 个叶节点,构造一棵二叉树。若该树的带权路径长度(WPL)最小,则称其为 最优二叉树(赫夫曼树、哈夫曼树、霍夫曼树)
-
节点的带权路径长度:该节点的权 × 节点路径长度
-
树的带权路径长度:所有的叶结点的带权路径长度之和
赫夫曼树中,一定是权值较大的节点距离根更近。
赫夫曼树的例子:
graph TD
A(NaN)---B(NaN)---C(14)
B---b(NaN)---c(5)
b---D(NaN)---E(1)
D---F(2)
A---a(NaN)---aa(16)
a---ab(20)#生成赫夫曼树:
- 对数据进行排序。每个数据都可以创建一个节点
- 取出权值最小的两颗二叉树,合并为一棵新的二叉树。该二叉树权值是两棵子树的权值之和
- 将数据再次排序,重复合并步骤,直至剩余唯一的树,即为赫夫曼树
#赫夫曼编码:
赫夫曼编码是一种编码方式,是一种程序算法。赫夫曼编码是赫夫曼树在电讯通信中的经典应用之一。
赫夫曼编码广泛应用于数据文件压缩,其压缩率在 20% ~ 90% 间
赫夫曼编码是可变字长编码的一种。是老赫在 1952 年提出的编码方法,称为 “最佳编码”
赫夫曼编码是无损处理方案。由于赫夫曼编码是按字节处理数据,因此可以处理所有文件
编码方式有三种:
-
定长编码:
如 ASCII 码,其每个字符占用长度为固定 8 字节
-
变长编码:
对字符进行统计,按照各个字符出现的次数进行编码。出现次数越多,编码越小。
字符的编码不能是其他字符编码的前缀,这样的编码叫做前缀编码(消除二义性)。
-
赫夫曼编码:
按照字符的出现次数,构建赫夫曼树。之后,按照赫夫曼树结构,给字符规定编码。向左的路径记为 0,向右记为 1。
这样得到的编码,一定是前缀编码。因为那些字符节点都是叶节点。赫夫曼行啊赫夫曼!
之后,用规定的编码将指定字符串转化为字节数组。最后,传递字符数组即可。
#实现赫夫曼编码:
——见本章附录:[F1 实现赫夫曼编码/解码]
注意事项:
- 压缩已经过压缩处理的文件,那个压缩率会变低
- 如果一个文件中重复的数据很少,压缩效果也会不明显
14.1.4 二叉排序树
二叉排序树(BST,Binary Sort Tree):对于任何一个非叶节点,其左节点小于等于当前节点,右节点大于等于当前节点
二叉排序树的例子:
graph TD
A(10)---B(8)
B---D(4)---c(2)---d(1)
D---b(6)
B---E(9)
A---C(15)---e(12)
C---ee(23)二叉排序树删除节点:
-
删除叶节点的场合,将那个父节点的对应连接置空即可。
-
删除有唯一子节点的节点场合,让那个父节点的对应连接改为指向子树即可。
-
删除有两个子节点的节点的场合,将该节点置为正无穷或负无穷。
之后维护该二叉排序树,直到该节点成为叶节点时,删除该节点即可。
#14.1.4.1 平衡二叉树
二叉排序树可能形成一些奇怪的形状(如左子树全部为空),这样就不能发挥树形结构的比较优势。
平衡二叉树(AVL 树):也叫平衡二叉搜索树。非空时,其任意节点左右两个子树的高度差不超过 1,且左右子树也都是平衡二叉树。
平衡二叉树的实现方法有:红黑树、AVL、替罪羊树、Treap、伸展树等
#平衡二叉树的左旋转:
- 创建一个新节点。该节点的值等于根节点值
- 使该新节点的左子树指向当前根节点的左子树。使该节点的右子树指向当前根节点右子树的左子树
- 使当前根节点的右子树的左子树指向该新节点
- 使当前根节点的右子树成为新的根节点。旧的根节点被废弃
简单的说,就是让根节点的右子树指向右子树的左子树。而右子树的左子树指向根节点。
合理性在于,根节点(root)的右子树(right)上的所有值都大于 root;而 right 的所有左子树的值,以及 root 所有左子树的值也一定小于 right 值
#平衡二叉树的右旋转:
还不是一样?
#平衡二叉树的双旋转:
符合进行右旋转的条件(右子树高度 > 左子树高度 + 1)时,如果那个左子树的右子树高度高于其左子树高度,需要先对左子树进行左旋转。以此类推。
#实现平衡二叉树:
——见本章附录:[F2 实现平衡二叉树]
14.1.5 线段树
线段树(Segment Tree)是一棵二叉树。其每个节点表示一个闭区间,父节点的区间内包含所有子节点的区间。
-
对于每个非叶节点,将其区间平均划分成两个子区间。左节点指向其中较小区间,右节点指向那个较大区间
换言之,对于非叶节点 [L, R],其左子节点是 [L, (L + R) / 2],右子节点是 [((L + R) / 2) + 1, R]
-
对于每个叶节点,其区间仅包含一个元素。即,其区间的左界等于右界。
线段树的例子:
在区间 [1, 9] 中,记录 [2, 9] 的样子
graph TB
Root([1,9])
Root---L([1,5])
style R fill: #BFFFFC
Root---R([6,9])
L---LL([1,3])
style LR fill: #BFFFFC
L---LR([4,5])
R---RL([6,7])
R---RR([8,9])
LL---LLL([1,2])
style LLR fill: #BFFFFC
LL---LLR([3,3])
LR---LRL([4,4])
LR---LRR([5,5])
RL---RLL([6,6])
RL---RLR([7,7])
RR---RRL([8,8])
RR---RRR([9,9])
LLL---LLLL([1,1])
style LLLR fill: #BFFFFC
LLL---LLLR([2,2])线段树是近似的完全二叉树。有时,线段树的节点是随着线段树的更新逐渐建立的,此时线段树不处于完全二叉树的状态。
线段树的更新:
标记区间时,按照 广度优先搜索 的思想,从根节点开始遍历区间。
——广度优先搜索,见本章 [14.3.2 广度优先搜索 BFS]
比如,添加区间 [START, END] 时:
-
如果一个节点的区间内所有元素都被标记,则标记这个节点
对于区间 [L, R],如果 L >= STRAT 且 R <= END,则标记该节点
-
如果一个节点的区间内部分元素被标记,则继续遍历其左右节点
对于区间 [L, R],MID = (L + R) / 2
如果 MID >= L,则需要遍历其左节点。如果 MID < R,则需要遍历其右节点
标记节点时,只需在该节点添加懒标记,而不必对所有子节点进行标记。
懒标记:
使用懒标记,可以只更新到满足条件的区间,而不必对所有子区间一一更新。此后再次遍历到该节点时,再对懒标记进行下推
上述例子中,记录区间 [2, 7] 时,仅更新了 [2, 2]、[3, 3]、[4, 5]、[6, 9] 这些节点。
以节点 [6, 9] 为例,该区间上被添加了懒标记,代表该区间及所有子区间都被记录了一次。下次遍历到这个节点时,懒标记被下推给子节点 [6, 7]、[8, 9]
线段树的查询:
一个区间的元素和,等于 其子区间各自元素和 的合计值
一个区间中的最大值,等于 其子区间各自最大值 中的较大值
14.2 多路查找树
二叉树虽然效率较高,但需要加载到内存中。节点过多时就可能出现问题。
如:需要进行多次 I / O 操作,导致构建速度慢;造成二叉树高度很大,降低操作速度。
每个节点可以拥有更多数据项和更多子节点的树,就是多叉树(multiway tree)。
多叉树通过重新组织节点,能减少树的高度,能对二叉树进行优化。
#名词解释:
- 节点的度:节点的子节点数量
- 树的度 / 阶:树中所有节点的度的最大值
14.2.1 2-3 树
2-3 树是最简单的 B 树结构。其具有如下特点:
-
所有叶节点都在同一层。节点包含不超过 2 个值。
-
有两个子节点的节点叫 二节点。二节点要么没有子节点,要么有两个子节点。
有三个子节点的节点叫 三节点。三节点要么没有子节点,要么有三个子节点。
-
2-3 树是由 二节点 和 三节点 构成的树。其节点仍遵循二叉排序树的规则。
对于二节点:其左子树的值需小于当前节点、右子树的值需大于当前节点
对于三节点:其左子树的值小于当前节点的最小值,中子树的值需介于当前节点的两个值之间,右子树的值大于当前节点的最大值
2-3 树的例子:
graph TD
A(10)---B(6)
B---D(1, 3)
B---E(7)
A---C(15, 20)
C---F(11, 12)
C---G(19)
C---H(22, 32)#构建 2-3 树:
-
插入节点时,如果不能满足条件,即需要拆分。
拆分时先拆上层。上层满时,才拆本层。拆分后仍要满足规则
#2-3-4 树:
还不是一样?
14.2.2 B 树
B 树(b-tree,balance tree)。2-3 树与 2-3-4 树都是 B 树的种类。
graph TD
ROOT(30, 60<br/>P1 - P2 - P3)
ROOT---R1(10, 20<br/>P1 - P2 - P3)
ROOT---R2(40, 50<br/>. - P2 - P3)
ROOT---R3(70, 80<br/>P1 - P2 - P3)
R1---R11(3, 6)
R1---R12(12, 13)
R1---R13(23, 24)
R2---R21( )
R2---R22(41, 48)
R2---R23(55, 57)
R3---R31(61, 62)
R3---R32(73, 74)
R3---R33(84, 86)B 树具有如下特点:
-
树树我啊,所有叶节点都在同一层呢。
-
搜索时,从根节点起,对当前节点内的关键字(有序)进行二分查找。
命中则结束。否则,进入那个对应范围的子节点。那个命中可能发生在叶节点,也可能在非叶节点。
如果当前节点为空,则表示没有找到。
-
B 树的关键字集合分布在整棵树中,非叶节点和叶节点都存放数据
-
B 树的搜索性能等价于在关键字全集内进行二分查找
#B+ 树:
B+ 树是 B 树的变体。
使用链表存储数据时,查找数据缓慢。因此将链表数据分为若干段,将每段的索引节点保存为树。
graph TD
ROOT(0, 32, 61<br/>A - B - C)
ROOT---R1(0, 12, 23<br/>A - B - C)
ROOT---R2(32, 40, 52<br/>A - B - C)
ROOT---R3(61, 73, 84<br/>A - B - C)
R1---R11(0<br/>4<br/>9)
R1---R12(12<br/>13<br/>17)
R1---R13(23<br/>24<br/>25)
R2---R21(32<br/>38<br/>39)
R2---R22(40<br/>41<br/>48)
R2---R23(52<br/>55<br/>57)
R3---R31(61<br/>62<br/>66)
R3---R32(73<br/>74<br/>79)
R3---R33(84<br/>86<br/>87)
subgraph 数据链表
R11
R12
R13
R21
R22
R23
R31
R32
R33
endB+ 树具有如下特点:
-
B+ 树的关键字都出现在叶节点的链表中,链表中数据是有序的。
非叶节点只相当于叶节点的索引(稀疏索引),叶节点相当于是存储数据的数据层(稠密索引)。
-
B+ 树的命中只可能发生在叶节点。
-
B+ 树的搜索性能也等价于在关键字全集内进行二分查找
-
B+ 树更适合文件索引系统
#B* 树:
B* 树是 B+ 树的变体,其在非根、非叶节点间加入了兄弟指针。
graph TD
ROOT(0, 32, 61<br/>A - B - C)
ROOT---R1(0, 12, 23<br/>A - B - C)
ROOT---R2(32, 40, 52<br/>A - B - C)
ROOT---R3(61, 73, 84<br/>A - B - C)
R1---R11(0<br/>4<br/>9)
R1---R12(12<br/>13<br/>17)
R1---R13(23<br/>24<br/>25)
R2---R21(32<br/>38<br/>39)
R2---R22(40<br/>41<br/>48)
R2---R23(52<br/>55<br/>57)
R3---R31(61<br/>62<br/>66)
R3---R32(73<br/>74<br/>79)
R3---R33(84<br/>86<br/>87)
subgraph 数据链表
R11
R12
R13
R21
R22
R23
R31
R32
R33
end
subgraph 索引相连
R1
R2
R3
endB* 树具有以下特点:
- B* 树定义了非叶子节点关键字个数至少为 (2 / 3) * M。其块的最低使用率为 2 / 3,而 B+ 树最低使用率为 1 / 2
- B* 树分配新节点的概率更低,空间使用率更高
14.2.3 前缀树
前缀树(字典树、单词查找树、键树),是一种多路查找树。利用元素的公共前缀来减少查询时间。
下面是一个存储了数个单词(a、act、art、cat、can、cant、roin)的前缀树:
graph TB
R[ ]
style a fill: #C0F0E0
R --- a((a))
R --- c[c]
R --- r[r]
a --- ac[c]
a --- ar[r]
style act fill: #C0F0E0
ac --- act((t))
style art fill: #C0F0E0
ar --- art((t))
c --- ca[a]
style cat fill: #C0F0E0
ca --- cat((t))
style can fill: #C0F0E0
ca --- can((n))
style cant fill: #C0F0E0
can --- cant((t))
r --- ro[o]
ro --- roi[i]
style roin fill: #C0F0E0
roi --- roin((n))前缀树具有如下特点:
-
根节点不包含字符,除根节点外每一个节点包含一个字符。
-
节点的路径即为一条存储字符串。特别的,根节点表示空字符串
每个节点持有一个计数器,计算该节点处存储的字符串数量。
-
所有的子节点都与父节点具有相同前缀。
-
在前缀树中,查询字符串的时间复杂度为 O(L),其中 L 为字符串长度
实现前缀树:
class TrimTree {
/* 节点类 */
private static class Node {
Map<Character, Node> next = null;
int count = 0;
Node() {
this.next = new HashMap<>();
this.count = 0;
}
}
private Node root = null; // 根节点
/* 构造器 */
public TrimTree(String... strings) {
this.root = new Node();
for (String s : strings) add(s);
}
/* 添加字符串 */
public void add(String s) {
Node p = root;
for (char c : s.toCharArray()) {
if (!p.next.containsKey(c)) p.next.put(c, new Node());
p = p.next.get(c);
}
p.count++;
}
/* 查找字符串 */
public int search(String s) {
Node p = root;
for (char c : s.toCharArray()) {
if (!p.next.containsKey(c)) return 0;
p = p.next.get(c);
}
return p.count;
}
}14.3 图
线性表局限于一个直接前驱和一个直接后继的关系。
树可能有数个直接后继,但只能有一个直接前驱(父节点)
当需要表示多对多关系时,就需要 图
图是一种数据结构。每个节点可以有零个或多个相邻元素。
两个节点间的连接称为 边(edge),节点也被称为 顶点(vertex)
图的分类:
- 按照 顶点间的连接有无方向 分为:有向图、无向图
- 按照 是否带权 分为:带权图(网)、非带权图
- 按照 表示方式 分为:二维数组表示(邻接矩阵)、链表表示(邻接表)
#图的表示方式:
一组连接的节点:
graph TD
A(1)---B(0)
A---C(2)
B---C
B---D(3)
B---E(4)邻接矩阵:
0 1 2 3 4
0 ┌0, 1, 1, 1, 1┐
1 |1, 0, 1, 0, 0|
2 |1, 1, 0, 0, 0|
3 |1, 0, 0, 0, 0|
4 └1, 0, 0, 0, 0┘其中,(0, 1) == 1 表示 节点 0 与 节点 1 相连
邻接矩阵为每个顶点都分配了 n 个边的空间。这样,造成了空间的损失
邻接表:
0 [1]→[2]→[3]→[4]→
1 [0]→[2]→
2 [0]→[1]→
3 [0]→
4 [0]→邻接表为每个节点创建一个链表,链表中是与其相连的节点。邻接表由 数组 + 链表 组成
邻接表只关心存在的边,不关心不存在的边,因此没有空间浪费
14.3.1 深度优先搜索 DFS
深度优先搜索(Depth First Search),其策略是优先纵向挖掘深入,而不是对一个节点的所有节点先进行横向访问。
从初始访问节点出发,首先访问其第一个相邻节点。之后,从那个访问节点出发,递归访问第一个相邻节点。直到一个节点的路径完全访问结束后,才访问第二个节点。
#步骤:
- 访问初始节点 s,标记其为已访问
- 从 s 的第一个相邻节点起,以递归方式对其进行深度优先搜索。
- 当前节点没有可访问的相邻节点时,就完成了对一条路径访问。此时才返回上一级,继续搜索下一节点。
14.3.2 广度优先搜索 BFS
广度优先搜索(Broad First Search),其策略是优先横向访问所有相邻节点,而不是对一条路径进行纵向挖掘。
从初始访问节点出发,记录所有相邻节点。之后,访问先前记录节点,并记录所有相邻节点。直到没有能访问的节点为止,就完成了对所有连接节点的搜索。
#步骤:
- 记录初始节点 s
- 访问上一次记录的节点,将其标记为已访问。将那些节点的所有可访问的相邻节点记录。
- 重复上一步,直到没有可访问的节点时,就完成了对所有连接节点的访问。
附录
F1 实现赫夫曼编码/解码
/* 压缩数据包 */
class DataBox {
public byte[] data; // 压缩信息主体
public Map<Byte, String> key; // 赫夫曼表
public int step; // 补位数
}
class Huff {
/* 将数据压缩,返回一个压缩包 */
public static DataBox huff(byte[] data) {
DataBox dataBox = new DataBox();
dataBox.key = getHuffMap(data); // 在压缩包内记录编码表
dataBox.data = toHuff(data, dataBox); // 在压缩包内记录压缩后数据,也会记录补位数
return dataBox;
}
/* 根据要压缩的数据,计算那个赫夫曼表 */
private static Map<Byte, String> getHuffMap(byte[] val) {
if (val == null || val.length == 0) return new HashMap<>();
Map<Byte, Node> huff = new HashMap<>();
for (byte c : val) { // 记录每个字符出现的次数
if (huff.containsKey(c)) huff.get(c).times++;
else huff.put(c, new Node(c, 1));
}
PriorityQueue<Node> pq = new PriorityQueue<>(huff.values());
while (pq.size() > 1) { // 生成赫夫曼树
Node temp = new Node(pq.remove(), pq.remove());
pq.add(temp);
}
Map<Byte, String> ret = new HashMap<>();
update(ret, pq.remove(), ""); // 根据那个赫夫曼树,生成赫夫曼编码
if (ret.size() == 1) ret.put(val[0], "0"); // 特别地,只有唯一字符从场合这样处理
return ret;
}
/* 根据赫夫曼表,将数据压缩 */
private static byte[] toHuff(byte[] val, DataBox d) {
StringBuilder sb = new StringBuilder();
for (byte c : val) { // 得到压缩后的 bit 字符串
sb.append(d.key.get(c));
}
byte[] ret = new byte[(sb.length() + 7) / 8]; // 压缩后的数据放在 byte 数组中
d.step = sb.length() % 8; // 记录那个补位数
for (int i = 0; i < ret.length; i ++) {
if (i >= ret.length - 1 && d.step != 0) { // 最后一位可能有补位。那个场合,让有效数字在最左侧
ret[i] = (byte) (Integer.parseInt(sb.substring(8 * i), 2) << (8 - d.step));
} else ret[i] = (byte) Integer.parseInt(sb.substring(8 * i, 8 * i + 8), 2);
}
return ret;
}
/* 该方法能遍历赫夫曼树,以获取赫夫曼表 */
private static void update(Map<Byte, String> ss, Node root, String s) {
if (root == null) return;
else if (root.right == null && root.left == null) {
ss.put(root.val, s); // 是叶节点的场合,记录这个编码值
}
if (root.left != null) update(ss, root.left, s + "0"); // 向左路径记为 0
if (root.right != null) update(ss, root.right, s + "1"); // 向右路径记为 1
}
/* 解压压缩包 */
public static byte[] antiHuff(DataBox d) {
StringBuilder sb = new StringBuilder();
for (int i = 0; i < d.data.length; i++) { // 获取那个压缩数据的编码
String temp = null;
if (i >= d.data.length - 1 && d.step != 0) sb.append((temp = Integer.toBinaryString(d.data[i] | 256)), temp.length() - 8, temp.length() - 8 + d.step); // 遍历到最后,要处理那个补位
else sb.append((temp = Integer.toBinaryString(d.data[i] | 256)).substring(temp.length() - 8));
}
Map<String, Byte> anti = new HashMap<>();
for (Byte aByte : d.key.keySet()) { // 将编码表转化为解码表
anti.put(d.key.get(aByte), aByte);
}
List<Byte> ret = new ArrayList<>();
StringBuilder s = new StringBuilder();
for (int i = 0; i < sb.length(); i++) { // 按照解码表,把压缩编码转化为未解压编码
s.append(sb.charAt(i));
if (anti.containsKey(s.toString())) {
ret.add(anti.get(s.toString()));
s = new StringBuilder();
}
}
byte[] bt = new byte[ret.size()]; // 将 Byte 数组转化为 byte 数组
for (int i = 0; i < bt.length; i++) {
bt[i] = ret.get(i);
}
return bt;
}
/* 节点类,是构建赫夫曼树时用到的类 */
static class Node implements Comparable<Node> {
public byte val; // 代表的 byte 值
public int times; // 出现的次数
public Node left;
public Node right;
public Node(Node l, Node r) {
this.left = l;
this.right = r;
this.times = l.times + r.times;
}
public Node(byte val, int pow) {
this.val = val;
this.times = pow;
}
public Node(byte val) {
this.val = val;
this.times = 0;
}
@Override
public int compareTo(Node o) {
return this.times - o.times;
}
}
}F2 实现平衡二叉树
class AVL{
public Node root = null; // 根节点
/* 添加一个值(添加一个节点)
val:要添加的值 */
public void add(int val) {
Node toAdd = new Node(val);
if (root == null) root = toAdd;
else {
Node par = root;
Node temp = root;
while (temp != null) { // 确定其插入位置
par = temp;
if (val > temp.val) {
temp = temp.right;
toAdd.way = true;
} else {
temp = temp.left;
toAdd.way = false;
}
}
if (toAdd.way) { // 将其插入到指定位置
par.right = toAdd;
par.right.parent = par;
} else {
par.left = toAdd;
par.left.parent = par;
}
while (true) { // 维护该平衡二叉树
par = toAVL(par);
if (par.parent == null) {
root = par;
break;
} else {
if (par.way) par.parent.right = par;
else par.parent.left = par;
par = par.parent;
}
}
}
}
/* 维护平衡二叉树
root: 待检查节点 */
private static Node toAVL(Node root) {
if (root == null) return null;
int gap = root.rightHeight() - root.leftHeight();
if (Math.abs(gap) > 1) { // |gap| > 1 时,需要旋转
if (gap > 0) { // gap > 0 需要左旋,否则右旋
if (root.right.leftHeight() > root.right.rightHeight()) root.right = roll(root.right, true);
return roll(root, false);
} else {
if (root.left.rightHeight() > root.left.leftHeight()) root.left = roll(root.left, false);
return roll(root, true);
}
} else return root;
}
/* 对该节点进行旋转。
root:待旋转节点
dirR:true 的场合右旋,否则左旋 */
private static Node roll(Node root, boolean dirR) {
Node temp = null;
if (dirR) {
temp = root.left;
root.left = temp.right;
if (temp.right != null) {
temp.right.way = false;
temp.right.parent = root;
}
temp.right = root;
} else {
temp = root.right;
root.right = temp.left;
if (temp.left != null) {
temp.left.way = true;
temp.left.parent = root;
}
temp.left = root;
}
temp.way = root.way;
temp.parent = root.parent;
root.way = dirR;
root.parent = temp;
return temp;
}
/* 一个展示树的方法。供 debug 用 */
public static void show(Node root) {
LinkedList<Node> a = new LinkedList<>();
LinkedList<Node> b = new LinkedList<>();
a.add(root);
while (!a.isEmpty()) {
Node temp = a.removeFirst();
System.out.print(temp.val + " ");
if (temp.left != null) b.add(temp.left);
if (temp.right != null) b.add(temp.right);
if (a.isEmpty()) {
System.out.println();
a = b;
b = new LinkedList<>();
}
}
System.out.println("共 " + count(root) + " 个节点");
}
/* 一个清点树中节点的方法 */
public static int count(Node root) {
if (root == null) return 0;
return 1 + count(root.left) + count(root.right);
}
public static class Node {
public int val; // 值
public Node left; // 左节点
public Node right; // 右节点
public Node parent; // 父节点
boolean way = false; // false:该节点是左节点;true:是右节点
public Node(int val) {
this.val = val;
}
public int leftHeight() { // 左子树高度
return (left == null ? 0 : left.height());
}
public int rightHeight() { // 右子树高度
return (right == null ? 0 : right.height());
}
public int height() { // 该节点树高度
return Math.max(leftHeight(), rightHeight()) + 1;
}
}
}