本文最后更新于：2024年4月9日下午

CA2 数据

机器级数据分为两类：

数值数据：无符号整数、带符号整数、浮点数
非数值数据：逻辑数（包括位串）、西文字符和汉字

计算机内部所有信息都用二进制进行编码。

使用二进制码的原因：制造两个稳定态的物理器件容易
二进制编码、计数、运算规则简单
1/0 正好与逻辑命题中的真/假对应，便于逻辑运算
可以方便地用逻辑电路实现算术运算

现实中真正的值称为真值，其在计算机内部的二进制数列称为 机器数

数据表示：计算机硬件能直接识别、指令可直接调用的数据类型。数据表示表现在其有对计算机硬件识别和引用的数据类型进行操作的指令和运算部件。

引入数据表示（添加硬件支持）取决于：系统效率（包括实现时间与存储空间）是否提高、数据通用性与利用率是否提高

数据结构：由软件进行处理和实现的各种数据类型。

CA2.1 二进制

数值数据的表示有三要素：进位计数制、定/浮点表示、二进制编码

#进位计数制

二进制（Binary，用后缀 0b 表示）、八进制（Octal，用后缀 O 表示）、十进制、十六进制（Hexadecimal，用后缀 H 或前缀 0x 表示）

日常生活中使用十进制，计算机中使用二进制。八进制与十六进制主要是二进制的简便表示。

对于 $R$ 进制数（ $R$ 是基数，可以是 $2、8、10、16$ 等），该数的右起第 $n$ 位的数值 $v$ 代表 $v\times R^{n-1}$ 。将数值的各位累加即该值的十进制表示。

对于 $R$ 进制浮点数，其尾数左起第 $n$ 位的数值 $v$ 代表 $v\times R^{-n}$ ，将尾数值的各位累加即该尾数的十进制表示。

#定/浮点表示

定点整数、定点小数、浮点数

计算机中只能通过约定小数点的位置来表示小数。其中：

定点数

小数点在固定位置的数。

定点小数通常用来表示浮点数的尾数部分。定点整数分为带符号整数或无符号整数
浮点数

小数点位置可浮动的数。

任何实数 $X$ 都能写成 $X=(-1)^S\times M\times R^E$ 的形式。

其中 $(-1)^S$ 决定该数的符号（正负）、 $M$ 是一个二进制的定点小数（尾数）、 $R$ 是基数、 $E$ 是一个二进制定点整数（阶、指数）

计算机中只要确定 $S,M,E$ 这三个信息，就能确定 $X$ 的值。这就是浮点数

#二进制编码

分为原码、补码、反码、移码

原码

正/负号用最左端的 0/1 表示，数值部分不变。

如：3（0011）、-3（1011）

原码有一些缺点：0 的表示不唯一、加减运算方式不统一、要额外对符号位进行处理等

所以，从 50 年代开始，整数都采用补码表示。但浮点数的尾数仍用原码定点小数表示
移码

将每个数值加上一个偏置常数。编码位数为 $n$ 时，偏置常数取 $2^{n-1}$ 或 $2^{n-1}-1$ 。

如： $n=4$ 时，偏置常数取 8。此时，-8（-8+8：0000B）、+6（+6+8：1110B）

此时，0 的移码表示唯一，且移码与补码仅第一位不同
补码
在模运算系统中，一个数与其取模的结果等价（时钟就是模 12 系统）。等价的数称为补码。

如： $-4\equiv8\quad(\operatorname{mod} 12)$ ，称：8 是 -4 对模 12 的补码

有以下结论：
- 一个负数的补码等于模减该负数的绝对值：
  
  对于某一确定的模 $M$ ，数值 $x(x<0)$ ，有 $x\equiv M-|x|\quad(\operatorname{mod}M)$
- 对于某一确定的模 $M$ ，数值 $x,y\,(y<M)$ ，有 $x-y\equiv x+(M-y)\quad(\operatorname{mod}M)$
于是，对于机器数 $[X]_补$ 和真值 $X$ ，有 $[X]_补\equiv 2^n+X\quad(-2^n\le X<2^n,\operatorname{mod}2^n)$

正数：符号位为 0，数值部分不变

负数：符号位为 1，数值部分按位取反，之后加 1

变形补码：符号位为 2 位，用于存放可能溢出的中间结果。

如：8（补码：1000、变形补码：01000）；-8（补码：1000、变形补码：11000）

CA2.2 定点数

机器中字的位排列顺序有两种方式，即高到低位可以是从右到左，也可能是从左到右。一般多采用从左往右排列方式。

为避免表达歧义，用 LSB（Least Significant Bit）来表示最低有效位，MSB 来表示最高有效位。

无符号整数：在全部是正数运算且不会出现负值的情况下，可以使用无符号数。如：地址运算、编号表示等。无符号整数的编码没有符号位。常在一个数后面加一个 U 或 u 表示无符号数

带符号整数：用 MSB 表示数字的符号（0 正数、1 负数）。通常使用补码表示带符号整数

若同时有无符号数和带符号数，C 语言会将带符号数强制转换成无符号数。

所以在 C 语言中，一些表达式会产生以下结果

关系表达式	类型	结果	说明
`0 == 0U`	无符号	True	$00\dots 0B（0）= 00\dots 0B（0）$
`-1 < 0`	带符号	True	$11\dots 1B（-1）< 00\dots 0B（0）$
`-1 < 0U`	无符号	False	$11\dots 1B（2^{32}-1）> 00\dots 0B（0）$
`2147483647 > -2147483647-1`	带符号	True	$011\dots 1B（2^{31}-1）> 100\dots 0B（-2^{31}）$
`2147483647U > -2147483647-1`	无符号	False	$011\dots 1B（2^{31}-1）< 100\dots 0B（2^{31}）$
`2147483647 > (int)2147483648U`	带符号	True	$011\dots 1B（2^{31}-1）> 100\dots 0B（-2^{31}）$

CA2.3 高级数据表示

#自定义数据表示

包含标识符的数据表示和数据描述符两类

标识符的数据表示

在计算机中的数据左侧添加标志位，以识别不同类型的数据

其优点是：简化了指令系统和程序设计、简化了编译程序、便于实现一致性校验、能由硬件自动变换数据类型、支持数据库系统的实现与数据类型无关的要求、为软件测试和应用开发提供支持

缺点是：每个数据字增设标识符，可能占用更多空间、采用标识符降低了指令执行速度
数据描述符

描述符与数据分开存放，用于描述要访问的数据的信息。

#向量、数组数据表示

增设向量、数组数据表示、硬件支持，做称向量机

引入向量、数组数据表示不只是能加快形成元素地址，还便于实现把向量各元素成块预取到中央处理机。

#堆栈数据表示

有堆栈数据表示的计算机称为堆栈计算机。

堆栈计算机有若干高寄存器组成的硬件堆栈，并附加控制电路，使其在主存中的堆栈区在逻辑上形成主体，使堆栈的访问速度是寄存器的，容量是主存的。

堆栈计算机有丰富的堆栈操作指令且功能强大，可直接对堆栈数据进行各种运算和处理

堆栈计算机有力支持了高级语言程序的编译。且有力支持了子程序的嵌套和递归调用。

#浮点数

在科学计数法中，任何数都能表示为类似 $2.022\times10^{3}$ 的格式。

一个数有多种表示形式，但规格化形式（小数点前只有一位非 0 数）是唯一的。

在二进制中，也能将数字表示为 $1.1111100101_{two}\times 2^{10}$ 的形式

32 位浮点数 (-1)^S × 1.xxxx × 2^E 的规格化数如下所示：

（CA2_3 浮点数结构图）

S：符号（正/负）
Exponent：阶码。
significant：有效数

早期各计算机内部浮点数的表示格式还不统一，因而互不兼容。

浮点数尾数的基值可表示数的范围、个数，随进制增大而增大。其精度随之减小，精度损失可能性也减少。

浮点数尾数下溢时，处理方法有：截断法、舍入法、恒置 1 法、查表舍入法。

IEEE 754

1985 年，IEEE 754 标准制定。现在所有通用计算机都采用 IEEE 754 来表示浮点数

单精度（SP）：(-1)^S × (1 + Significant) × 2^{(Exponent - 127)}

双精度（DP）：(-1)^S × (1 + Significant) × 2^{(Exponent - 1223)}

（CA2_3_1 单精度浮点数图）

S：符号，1 位。1 表示负值，0 表示正值
Exponent：阶码。用移码表示。全 0 和全 1 表示特殊值

单精度 8 位。偏置常数为 127。范围为 -126（0000 0001）~ 127（1111 1110）

双精度时 11 位，偏置常数为 1023。
significant：有效数（尾数的小数点后部分）

多数情况下，科学计数法小数点前一位总是 1，因此将尾数的第一位省略。剩余部分为有效数

要注意：规格化尾数的小数点后第一位总是 1；相对的，非规格化尾数的小数点后第一位总是 0

单精度时为 23 位。能用 23 位尾数表示 24 位数。

双精度时为 52 位。

如下表：

阶码（E）	有效数（M）	特殊值
全 1（255）	0	正负无穷大（取决于符号）
全 1（255）	非 0	非数（NaN）
0	0	正负零（取决于符号）
0	非 0	非规格化数：阶码视为取 1（即 -126 / -1022），尾数第一位为 0
非全 1 全 0	任意	规格化数：尾数第一位为 1

当数据是一个不可表示数时，机器将其转换为最近的可表示数。

CA2.4 非数值数据

#逻辑数据

逻辑数据用于表示表达式中的逻辑值（真/假）

表示：用 1 位表示。N 位二进制数可以表示 N 个逻辑数据
运算：按位进行。如按位与/或等。
识别：逻辑数据和数值数据在形式上无差别。计算机依靠指令来识别

#西文字符

西文字符是拼音文字，用有限字母就能拼出所有单词。字符总数不超过 256 个，可以使用 7-8 位二进制表示

表示：常用编码为 7 位 ASCII 码
操作：字符串操作。如传送、比较等

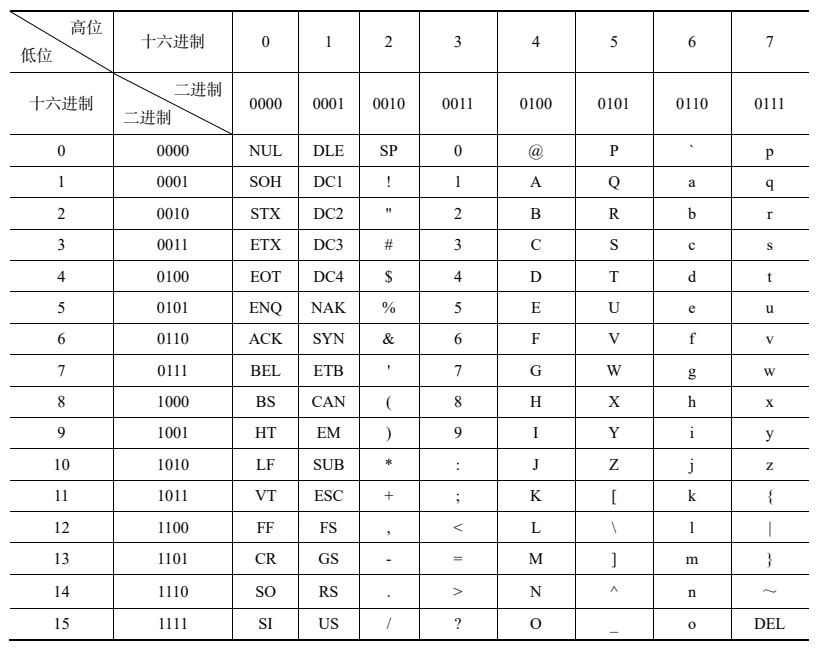
ASCII 码表如下：

（CA2_4 ASCII 码表）

如，空格（SP）的 ASCII 码为（0010 0000），字母 M 的 ASCII 码为（0100 1101）

#汉字

汉字数量巨大，总数超过 6 万字。

编码形式：有几种不同的编码形式
- 输入码：对汉字用相应按键进行编码表示。用于输入
- 内码：用于在系统中进行存储、查找、传送等处理
- 字模点阵或轮廓描述：描述汉字字模点阵或轮廓，用于显示/打印
GB2312-80 字符集
- 组成
  
  字母、数字和符号。包括英文、俄文、日文平假名与片假名、罗马字母、汉语拼音等共 687 个
  
  一级常用汉字，共 3755 个。按汉语拼音排列
  
  二级常用汉字，共 3008 个。按偏旁部首排列
- 区位码
  
  码表由 94 行，94 列组成。行号为区号，列号为位号。各占 7 位
- 国标码
  
  每个汉字的区号、位号各自加上 32 就得到了国标码。
  
  国标码的区号和位号各占 7 位，在前方添 1（为与 ASCII 码区别）构成字节。一个汉字占 2 字节

#多媒体信息的表示

图形、图像、音频、视频等信息

图形：用构建图形的直线或曲线的坐标点及控制点来描述。这些坐标点或控制点用数值数据描述
图像：用构成图像的点（像素）的亮度、颜色、灰度等信息描述。亮度等值用数值数据描述
音频：音频信息对模拟声音进行采样、量化（二进制编码）来获得。因此量化后得到的是一个数值数据序列
视频：随时间变化的图像（每幅图像称为一帧）
音乐：通过对演奏的乐器、乐谱等相关各类信息用 0、1 编码来描述

CA2.5 数据的存储

#数据的宽度

比特（bit，位）：是计算机中处理、存储、传输信息的最小单位。一位是就一个 0 或 1
字节（Byte，B）：二进制信息的基本计量单位。多数情况下，一个字节长 8 位。

现代计算机中，存储器按照字节编址。字节是最小可寻址单位

若以字节为一个排列单位，则 LSB 表示最低有效字节，MSB 表示最高有效字节
字（word）：用于表示其自然的数据单位的术语。字与字长的宽度可能相同或不同。

对于 x86 体系结构，不论字长多少，字都是 16 位。

对于 MIPS 32 体系结构，字和字长都是 32 位
字长：数据通路的宽度，CPU 一次能并行处理的二进制位数。

字长是 8 的倍数。常见有 16位、32位、64位。

数据通路是 CPU 内部数据运算、存储、传送的部件。这些部件需要宽度一致。
容量常用的单位

千字节（KB，1 KB = 2¹⁰ B = 1204 B）

兆字节（MB，1 MB = 2²⁰ B = 1204 KB）

千兆字节（GB，1 GB = 2³⁰ B = 1204 MB）

兆兆字节（TB，1 TB = 2⁴⁰ B = 1204 GB）
带宽常用的单位

千比特每秒（kb/s，1kbps = 10³ b/s = 1000 bps）

兆比特每秒（Mb/s，1Mbps = 10⁶ b/s = 1000 kbps）

千兆比特每秒（Gb/s，1Gbps = 10⁹ b/s = 1000 Mbps）

兆兆比特每秒（Tb/s，1Tbps = 10¹² b/s = 1000 Gbps）

把上述 b 换为 B 才表示字节，如 10 MBps 表示 10 兆字节/秒

高级语言支持多种不同的类型和长度的数据。

不同机器上表示同一种类型的数据分配的宽度，可能随 ISA、机器字长和编译器不同而不同。

#数据的存储

从 80 年代起，几乎所有通用计算机采用 字节编址

在高级语言中声明的基本数据类型有各种不同长度的数据，一个基本数据可能占用多个存储单元。存放方式有两种

大端方式：MSB 所在地址是数的地址
小端方式：LSB 所在地址是数的地址

有的机器支持两种存放方式，通过特定控制位来设定具体采用的方式。

C 语言的 union 的存放顺序是所有成员从低地址开始。可以以此测试 CPU 的大/小端方式

#寻址方式

通常要在指令中为每个操作数设置一个地址字段，以表示数据来源或去向的地址。指令中给出的是 形式地址，要用其计算出 实际地址。

寻址对象有以下几种：

面向寄存器：操作数可以取自寄存器或主存。结果多保存在寄存器中，少量送入主存。
面向堆栈：主要访问堆栈，少量访问主存或寄存器
面向主存：主要访问主存，少量访问寄存器
面向 I/O

寻址方式有以下几种：

立即数寻址：直接给出地址
直接寻址 / 绝对寻址：给出存放在主存中的地址位置的地址
寄存器直接寻址：给出寄存器地址，该寄存器中存放地址
寄存器间接寻址：给出寄存器地址，该寄存器中存放主存中地址位置的地址
存储器间接寻址：给出主存地址，该地址下保存地址位置
变址寻址：指令中给出地址码，并从指定寄存器中找到基址。用于数组
相对寻址：相对于当前 PC 寄存器的地址进行加减。用于分支跳转
基址寻址：指令中给出地址吗，并从基地址寄存器中取出基址。用于虚拟存储
堆栈寻址：堆栈是一个先进后出队列，不给出地址，而是操作指针

为指明寻址方式，可以占用操作码的某些位进行说明，也能在地址码部分专设寻址方式字段来指明。

程序在主存中的定位技术有：

静态重定位：目的程序装入主存时，通过软件（编译器）将逻辑地址转换为物理地址
动态重定位：指令不修改，通过基址寻址法来解决。要注意进行越界分析
虚实地址映像表：建立虚实地址映像表，通过查表获得物理地址

CA2.6 数据的运算

关于 0 和 1 的一套数学运算体系称为 布尔代数。

0 和 1 分别代表逻辑的 “假” 和 “真”。通过逻辑关系可以构建基于 0 和 1 的布尔代数运算。

基本的逻辑运算有：与（AND， $\bull$ ）、或（OR， $+$ ）、非（NOT， $\overline{ }$ ）

——见离散数学 [DM1 逻辑关系]、[DM4.7.4 布尔代数]

任何表达逻辑都能写成这三种运算的组合。

如异或（XOR， $\oplus$ ）逻辑表达式为： $A\oplus B=\overline{A}\bull B+A\bull \overline{B}$

#基本逻辑门电路

可以通过逻辑门电路来实现逻辑运算。

有三种基本门电路：与门、或门、非门

用这三种基本门电路就能组成其他门电路

（CA2_6 基本逻辑电路图1）

对于 n 位的逻辑运算，只要重复使用 n 个相同的门电路即可。

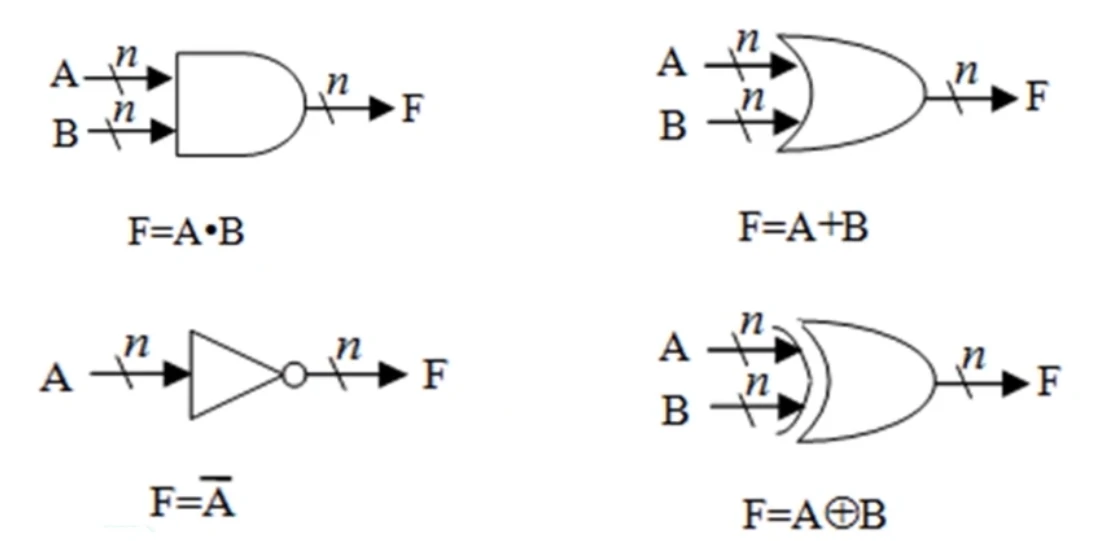
对于 n 位的逻辑值，那些逻辑符号如下所示

（CA2_6 基本逻辑电路图2）

#逻辑组合部件（功能部件）

根据电路是否有存储功能，将逻辑电路划分为以下两种

逻辑组合电路：没有存储功能，其输出仅依赖当前输入
时序逻辑电路：具有存储功能，其输出不仅依赖当前输入，还依赖存储单元的当前状态

可以利用基本逻辑门电路构成一些具有特定功能的 组合逻辑部件（功能部件）。如译码器、编码器、多路选择器、加法器等。

实现功能部件的过程：使用真值表描述功能部件输入与输出间的关系。再根据真值表确定逻辑表达式根据逻辑表达式实现逻辑电路

多路选择器（MUX）

二路选择器

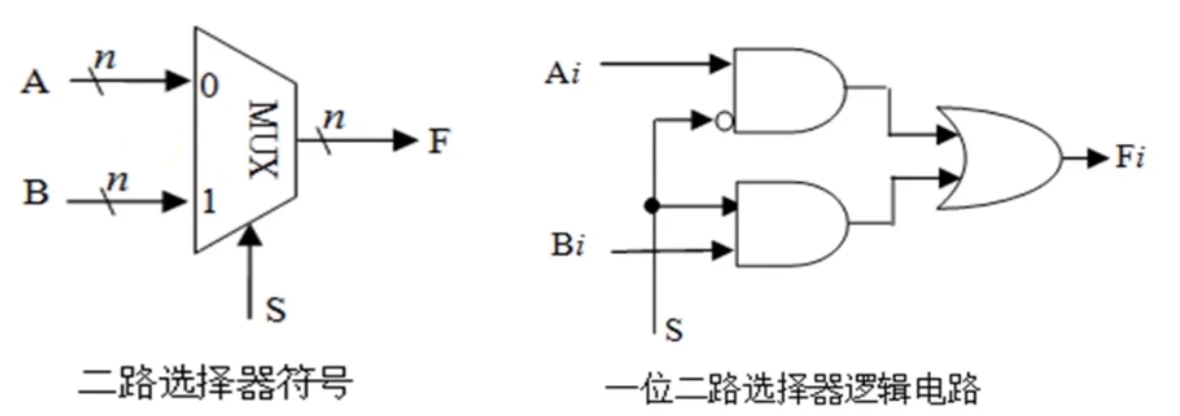
最简单的多路选择器。有输入端 $A,B$ ，控制端 $S$ 。输出端 $F=\begin{cases}A,&S=0\\B,&S=1 \end{cases}$

（CA2_6 二路选择器图）

k 路选择器

有 k 路输入，其控制端位数应是 $\log_2 k$
加法器

一位加法器称为全加器：有输入端 $A,B$ ，低位进位 ${Cin}$ ，和为 $F$ ，向高位进位为 ${Cout}$

有 $F=A\oplus B\oplus {Cin},\quad {Cout}=A\bull B+A\bull{Cin}+B\bull{Cin}$

（CA2_6 全加器图)

使用 n 个全加器就能实现 n 位加法器

（CA2_6 加法器图)
带标志加法器

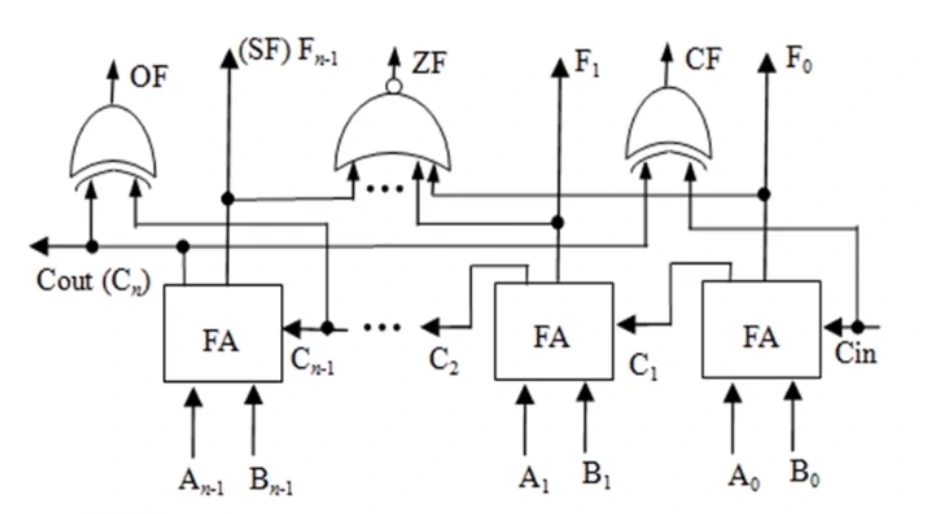
n 位加法器无法用于两个带符号整数（补码）加法，无法判断溢出。在程序中常要比较大小，这些可以通过减法得到的标志信息判断。带标志加法器 如下所示

（CA2_6 带标志加法器图)

其中标志：
- OF（溢出标志）： ${OF}=C_n\oplus C_{n-1}$ 。
  
  其中 $C_n$ 代表最高位进位， $C_{n-1}$ 代表次高位进位
  
  同符号数相加后，结果不同号，则为 1。异号数相加必定为 0
- SF（符号标志）： ${SF}=F_{n-1}$
  
  结果的第一位作为符号位
- ZF（零标志）： ${ZF}=1\oplus(F_0+F_1+\ldots+F_{n-1})$
  
  结果为 0 时 $ZF=1$
- CF（进/错位标志）： ${CF}={Cout}\oplus{Cin}$
  
  $Cout$ 即最高位进位 $C_n$ 。
  
  对于减运算，初始 $Cin=1$ ， $CF$ 表示借位。
  
  对于加运算，初始 $Cin=0$ ， $CF$ 表示进位。
进行补码运算有 $[A+B]_补=[A]_补+[B]_补,\quad [A-B]_补=[A]_补+[-B]_补$

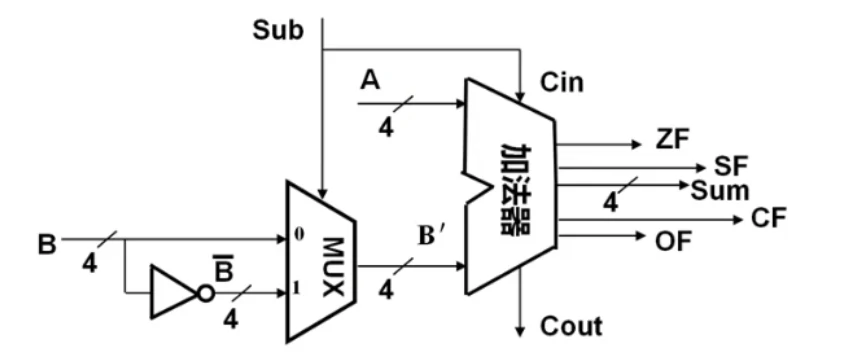
又因为 $[-B]_补=\overline{[B]_补}+1$ ，于是 整数加/减法运算器 就如下所示

（CA2_6 整数加减运算器图)

当 $Sub$ 为 1 时进行减法， $Sub$ 为 0 时进行加法。

在整数加/减运算部件基础上，加上寄存器、移位器、控制逻辑等，就能实现 ALU、乘/除运算、浮点运算 电路
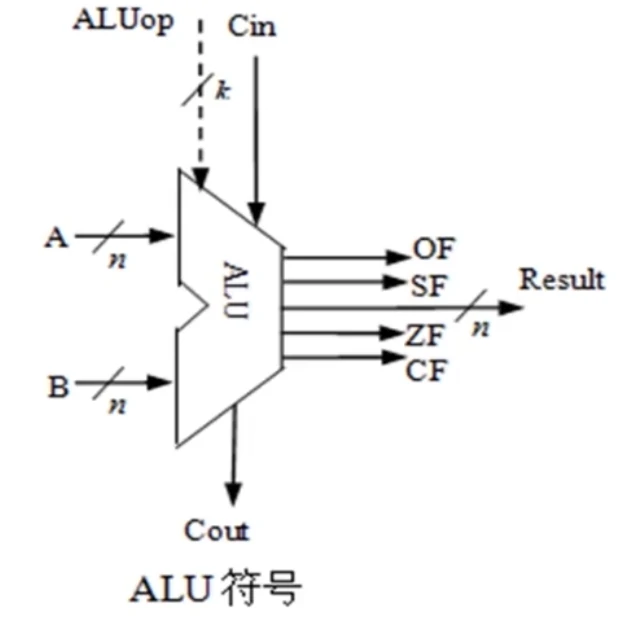
算术逻辑部件（ALU）

ALU（算术逻辑部件）的核心电路是带标志加法器。可以进行：
- 无符号整数加、减
- 带符号整数加、减
- 与、或、非、异或等逻辑运算
(CA2_6 ALU图)

有一个操作控制端（ALUop）用以决定 ALU 执行的处理功能。ALUop 的位数决定了操作的种类。

ALUop 为 3 位时，ALU 最多执行 $2^3=8$ 种操作

#从表达式到逻辑电路

C 语言中的基本数据类型、基本运算类型如下

基本数据类型
- 无符号数（二进制位串）、带符号整数（补码）
- 浮点数（IEEE 754 标准）
- 位串、字符（串）
基本运算类型
- 算数（+、-、*、/、%、>、<、<=、>=、==、!=）
- 位运算（|、&、~、^）
- 逻辑运算（||、&&、!）
- 移位（<<、>>）
- 扩展（无符号数高位加 0，带符号数按符号扩展）和截断（高位丢弃）

在进行运算时，先将表达式转换为指令序列。计算机执行指令，让操作数在运算电路中运算。

#整数加运算

整数加运算时，条件标志（零标志ZF、溢出标志OF、进/错位标志CF、符号标志SF）在运算电路中产生，被记录到专门的寄存器中。这些寄存器称为 程序/状态字寄存器（也叫标志寄存器）。每个标志对应寄存器中的一个标志位。

在无符号加法中，判断溢出的条件是 $CF=1$ ；在带符号加法中，判断溢出的条件是 $OF=1$

减法可以用于比较大小。无符号的场合，若 $CF=0$ 则被减数大于减数。带符号的场合，如果 $OF=SF$ 则被减数大于减数

下面是一个例子，下面的例子中假定 int 是 8 位。

/* 以下假定 n = 8，即 int 为 8 位 */

unsigned int x = 134;		// x 的机器数  1000 0110，真值为 134
unsigned int y = 246;		// y 的机器数  1111 0110，真值为 246
int m = x;					// m 的机器数  1000 0110，真值为 -6
int n = y;					// n 的机器数  1111 0110，真值为 -118

unsigned int z1 = x-y;
int k1 = m-n;
/*
  A         1000 0110
  B       + 0000 1001
  sub     +         1
        ——————————————————
            1001 0000         SF 1   OF 0   CF 1
  SF：符号位，结果为 1
  OF：进位为 0，次高位进位为 0，结果为 0
  CF：sub=1，进位为 0，结果为 1
  无符号数 CF=1 判断溢出，z1 = 144
  带符号数 OF=0 判断没有溢出，k1 = -112
*/

unsigned int z2 = x+y;
int k2 = m+n;
/*
  A         1000 0110
  B       + 1111 0110
  sub     +         0
        ——————————————————
            0111 1100         SF 0   OF 1   CF 1
  无符号数 CF=1 判断溢出，z2 = 124
  带符号数 OF=1 判断溢出，k2 = 124
*/

#整数乘运算

两个 n 位的二进制无符号数相乘，结果通常是 2n 位。

高级语言的两个 n 位数相乘，其结果通常只取乘积中的较低 n 位。

计算机内部，对于浮点数定有 $x^2\ge 0$ ，但带符号整数却不一定。

对于 $X\times Y$ ，取低 n 位作为结果，若高 n 位全部等于低 n 位的最高位则不溢出，否则溢出。

硬件不判断溢出。仅保留 2n 位乘积，供软件使用
如果程序不采用防止溢出的措施，且编译器也不生成处理溢出的代码，就可能出现问题
指令：分为无符号乘指令，带符号乘指令
乘法指令的操作数长度为 n，乘积长度为 2n。乘法指令不生成溢出标志，而以 2n 位乘积判断是否溢出
整数乘法运算比起位移和加法运算所用时间长得多。通常高级语言编译器处理变量与常数相乘时，会将其转化为移位、加法、减法的组合运算
不论无符号数还是带符号数的乘法，即使乘积溢出时，利用移位和加减运算组合得到的结果都是一样的

☆

#整数除运算

对于带符号整数来讲，n 位整数除以 n 位整数，除 $-2^{n-1}/{-1}=2^{n-1}$ 会溢出外，都不会溢出

整数除法的商也是整数，因此，不能整除时要进行舍入。舍入时会直接丢弃小数点后部分（截断）。

整数除法不能除以 0，否则会发生异常。

计算机中的整数除法运算比乘法运算用时更长，也不能通过流水线方式实现。为缩短除法运算时间，编译器处理除数为 2 的幂次形式时，采用右移运算实现。

能整除时，右移得到结果，移出为全 0。不能整除时，对于无符号数低位截断，有符号数加偏移量（ $2^k-1$ ）右移后再低位截断。

#浮点数加减运算

若两个浮点数分别为 $A=M_a\times 2^{E_a}\quad B=M_b\times 2^{E_b}\quad(E_a\ge E_b)$ ，则有

$A+B=(M_a+M_b\times2^{R_a-E_b})\times 2^{E_a}\\ A*B=(M_a \times M_b)\times 2^{E_a + E_b}\\ A/B=(M_a/M_b)\times 2^{E_a - E_b}$

上述运算可能出现几种情况

阶码上溢：一个正指数超过最大允许值（ $+\infin$ 、 $-\infin$ 、溢出）
阶码下溢：一个负指数超过最小允许值（+0、-0）
尾数溢出：最高有效位有进位（右规）
非规格化尾数：数值部分高位为零（左规）
右规或对阶时，右端有效位丢失（尾数舍入）

IEEE 建议实现时为每种异常情况提供一个自陷允许位。若某异常对应的位是 1，则发生相应异常时，调用一个特定的异常处理程序。异常情况有

无效运算（无意义运算）
- 运算时有一个数是非有限数
- 结果无效（ $NaN$ 、 $0/0$ 、 $x/0$ 、 $\infin/x$ ）
除以零（无穷大）
数太大（阶上溢）：对于 SP（单精度浮点数），指阶码 $E>1111\,\,1110$ （指数大于 127）
数太小（阶下溢）：对于 SP（单精度浮点数），指阶码 $E<0000\,\,0001$ （指数小于 -126）
结果不精确（舍入时引起），如 1/3、1/10 等不能精确表示成浮点数

进行浮点数加减法的步骤。（ $x\pm y$ ，其中 $M_x,\,E_x$ 是 $x$ 的尾数和阶数）

求阶差： $\Delta E= E_y - E_x$ （若 $E_y>E_x$ ，则结果阶码位 $E_y$ ）
对阶：将 $M_x$ 右移 $\Delta E$ 位，尾数变为 $M_x\times 2^{E_x-E_y}$
尾数加减： $M_x\times 2^{E_x-E_y}\pm M_y$
规格化：

当尾数高位为 0，则需要左规（尾数左移 1 次，阶码减 1，直到 MSB 为 1。每次移动后判断阶码是否下溢）

当尾数高位有进位，则需要右规（尾数右移 1 次，阶码加 1，直到 MSB 为 1。每次右移判断阶码是否上溢）

阶码溢出异常处理：上溢则结果溢出，下溢则结果为 0
若尾数比规定位数长，则舍入。若运算结果尾数为 0，则阶码也置 0。

IEEE754 规定，中间结果必须在右侧加 2 个有效位（一位保护位，一位舍入位）

舍入方式有几种
- 就近舍入：非中间值时正常舍入；恰为中间值则取最近偶数（其余部分奇数则入，为偶数则舍弃）
- 朝 $+\infin$ 舍入
- 朝 $-\infin$ 舍入
- 朝 0 舍入（直接丢弃）

计算机系统结构

#笔记 #基础课目 #计算机系统结构

<计算机系统结构>CA2 数据

https://i-melody.github.io/2022/12/13/计算机系统结构/2 数据/

作者

Melody

发布于

2022年12月13日

许可协议