<高等数学>证明集

AM 高等数学 证明集

AM1 函数与极限

收敛数列

收敛数列的极限是唯一的

设收敛数列 $\{x_n\}$ 存在极限 $a,b$ 且 $a\not= b$

则对于 $a,b$ 分别存在 $N$ 使 $\forall\epsilon>0,\forall n>N$，有 $\left| x_n-a\right| <\epsilon$ 和 $\begin{vmatrix}x_n-b\end{vmatrix}<\epsilon$

取 $\epsilon = \dfrac{b-a}{2}$

带入 $\begin{vmatrix}x_n-a\end{vmatrix}<\epsilon$ 有：$-\dfrac{3a-b}{2}<x_n<\dfrac{b+a}{2}$

同理带入 $\begin{vmatrix}x_n-b\end{vmatrix}<\epsilon$ 有：$\dfrac{b+a}{2}<x_n<\dfrac{3b-a}{2}$

则 $\dfrac{b+a}{2}<x_n<\dfrac{b+a}{2}$，矛盾

由此可知，收敛数列 $\{x_n\}$ 的极限唯一

收敛数列必定有界

若收敛数列 $\{x_n\}$ 的极限为 ${\lim_{n\rarr\infin} \\ } x_n=a$，则存在 $N$ 使得 $\forall\epsilon>0,\forall n>N$，$\begin{vmatrix}x_n-a\end{vmatrix}<\epsilon$。

取 $\epsilon = 1$，则 $\forall n>N$ 有 $\begin{vmatrix}x_n-a\end{vmatrix}<1$

可见 $\begin{vmatrix}x_n\end{vmatrix}=\begin{vmatrix}x_n-a+a\end{vmatrix}\le \begin{vmatrix}x_n-a\end{vmatrix}+\begin{vmatrix}a\end{vmatrix}\le 1+\begin{vmatrix}a\end{vmatrix}$

取 $M=\max(x_1,x_2,\ldots,x_{n-1},1+\begin{vmatrix}a\end{vmatrix})$，则 $\forall x\in\{x_n\}$ 都有 $x\le M$

收敛数列具有保号性

若收敛数列 $\{x_n\}$ 的极限为 ${\lim_{n\rarr\infin} \\ } x_n=a$，则存在 $N$ 使得 $\forall\epsilon>0,\forall n>N$，$\begin{vmatrix}x_n-a\end{vmatrix}<\epsilon$。

$a>0$ 时，取 $\epsilon = \dfrac{a}{2}$，则 $\forall n>N$ 有 $\begin{vmatrix}x_n-a\end{vmatrix}<\dfrac{a}{2}$

可见此时 $0<\dfrac{a}{2}<x_n<\dfrac{3a}{2}$

若 $a<0$ 时，同理可证 $\dfrac{3a}{2}<x_n<\dfrac{a}{2}<0$

收敛数列的任一子数列都收敛于同一极限

若收敛数列 $\{x_n\}$ 的极限为 ${\lim_{n\rarr\infin} \\ } x_n=a$，则存在 $N$ 使得 $\forall\epsilon>0,\forall n>N$，$\begin{vmatrix}x_n-a\end{vmatrix}<\epsilon$。

记其子数列为 $\{a_k\}$，对应关系为 $a_k=x_{n_k}$。

取 $K=N$，则对于 $\forall k>K$，有 $k>K=N$，以及 $a_k=x_{n_k}$

显然 $n_k>n_K=n_N\ge N$

故 $\begin{vmatrix}a_k-a\end{vmatrix}=\begin{vmatrix}x_{n_k}-a\end{vmatrix}<\epsilon$

即，存在 $K$ 使得 $\forall\epsilon>0,\forall k>K$，$\begin{vmatrix}a_k-a\end{vmatrix}<\epsilon$。

由此可知，子数列 $\{a_k\}$ 与数列 $\{x_n\}$ 都收敛于 $a$

函数的极限

一些重要极限（#1）

对于 $0<x<\dfrac{\pi}{2}$ 时，必有 $\sin x< x< \tan x$，即 $1<\dfrac{x}{\sin x}<\dfrac{1}{\cos x}$

当 $x\rarr 0$ 时，有 ${\lim_{x\rarr 0} \\ } \dfrac{1}{\cos x}=1$。显然也有 ${\lim_{x\rarr 0} \\ }1=1$

故有 ${\lim_{x\rarr 0} \\ }\dfrac{x}{\sin x}=1$

则 ${\lim_{x\rarr 0} \\ }\dfrac{\sin x}{x}={\lim_{x\rarr 0} \\ }\dfrac{1}{\dfrac{\sin x}{x}}=\dfrac{1}{ {\lim}\dfrac{x}{\sin x} }=\dfrac{1}{1}=1$

一些重要极限（#2）

人们将 ${\lim_{x\rarr \infin} \\}(1+\dfrac{1}{x})^x$ 的值定义为 $e$

下面是证明 ${\lim_{x\rarr \infin} \\}(1+\dfrac{1}{x})^x$ 存在且为常数。现给出两种证明方法

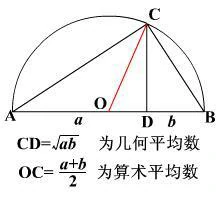
方法一：利用几何平均数和算数平均数

平均数关系图_AMZ_1.2.2

几何平均数小于等于算术平均数：$\sqrt[n]{a_1a_2\ldots a_n}\le\dfrac{a_1+a_2+\ldots+a_n}{n}$

下证 $(1+\dfrac{1}{x})^x$ 单调

对于数列 $a_x=(1+\dfrac 1{x})^x$，构建以下不等式：

$\sqrt[x+1]{1\times(1+\dfrac{1}{x})^x}\le\dfrac{1+x(1+\dfrac{1}{x})}{x+1}=\dfrac{x+2}{x+1}=1+\dfrac{1}{x+1}$

就有 $1\times(1+\dfrac{1}{x})^x\le(1+\dfrac{1}{x+1})^{x+1}$

即 $a_x<a_{x+1}$，则数列 $\{a_x\}$ 单调递增

下证 $(1+\dfrac{1}{x})^x$ 有界

构建数列 $b_x=(1+\dfrac 1{x})^{x+1}$，可见 $\{b_x\}>\{a_x\}$。可以构建以下不等式：

$\sqrt[x]{(1+\dfrac{1}{x})^2(1+\dfrac 1 x)^{x-1}}\le\dfrac{(1+\dfrac 1 x)^2+(x-1)(1+\dfrac 1 x)}{x}=1+\dfrac{x^2+x+1}{x^3}=1+\dfrac{x^3-1}{x^3(x-1)}<1+\dfrac{1}{x-1}$

就有 ${(1+\dfrac{1}{x})^2(1+\dfrac 1 x)^{x-1}}<(1+\dfrac{1}{x-1})^x$

即 $b_x<b_{x-1}$，则数列 $\{b_x\}$ 单调递减

由于 $b_1=4$，可见 $a_x<b_x\le4$

故 $\{a_x\}$ 上界存在。而显然 $a_x>0$，其下界存在。故 $\{a_x\}$ 有界

$\{a_x\}$ 单调递增，且有界，故 $\{a_x\}$ 的极限存在。人为定义 ${\lim_{x\rarr \infin} \\}(1+\dfrac{1}{x})^x=e$

方法二：利用二项式展开

二项式展开公式：$(a+b)^n=C^0_na^nb^0+C^1_na^{n-1}b^1+\ldots+C^r_na^{n-r}b^r+\ldots+C^n_na^0b^n$

下证 $(1+\dfrac{1}{x})^x$ 单调

对于数列 $a_x=(1+\dfrac{1}{x})^x$ 进行二项式展开，可得

${a_x}=(1+\dfrac{1}{x})^x=C^0_x+C^1_x\dfrac{1}{x}+\ldots+C^r_x\dfrac{1}{x^r}+\ldots+C^x_x\dfrac{1}{x^x}$

而 $a_{x+1}=(1+\dfrac{1}{x+1} )^{x+1}=C^0_{x+1}+C^1_{x+1}\dfrac{1}{x+1}+\ldots+C^r_{x+1}\dfrac{1}{(x+1)^r}+\ldots+C^{x+1}_{x+1}\dfrac{1}{ (x+1)^{x+1} }$

对于 $\forall r\in Z\le x$，有

$C^r_x\dfrac{1}{x^r}=\dfrac{x(x-1)\ldots(x-r+1)}{r!x^r}=\dfrac{1}{r!}\dfrac{x}{x}\dfrac{x-1}{x}\ldots\dfrac{x-r+1}{x}=\dfrac{1}{r!}(1-\dfrac{1}{x})(1-\dfrac{2}{x})\ldots(1-\dfrac{r-1}{x})$

和 $C^r_{x+1}\dfrac{1}{(x+1)^r}=\dfrac{(x+1)x(x-1)\ldots(x-r+2)}{r!(x+1)^r}=\dfrac{1}{r!}(1-\dfrac{1}{x+1})(1-\dfrac{2}{x+1})\ldots(1-\dfrac{r-1}{x+1})$

可见，$C^r_{x+1}\dfrac{1}{(x+1)^r}> C^r_x\dfrac{1}{x^r}$，于是数列 $\{a_x\}$ 单调递增。

下证 $(1+\dfrac{1}{x})^x$ 有界

又有 $C^r_x\dfrac{1}{x^r}=\dfrac{x(x-1)\ldots(x-r+1)}{r!x^r}<\dfrac{x^r}{r!x^r}=\dfrac{1}{r!}=\dfrac{1}{1\times 2\times\ldots\times r}<\dfrac{1}{2^{r-1}}$

则 $a_x=C^0_x+C^1_x\dfrac{1}{x}+\ldots+C^r_x\dfrac{1}{x^r}+\ldots+C^x_x\dfrac{1}{x^x}<1+\dfrac{1}{2^0}+\dfrac{1}{2^1}+\ldots+\dfrac{1}{2^{x-1} }<3$

可见，数列 $\{a_x\}$ 上界存在。而显然 $a_x>0$，其下界存在。故 $\{a_x\}$ 有界

$\{a_x\}$ 单调递增，且有界，故 $\{a_x\}$ 的极限存在。人为定义 ${\lim_{x\rarr \infin} \\}(1+\dfrac{1}{x})^x=e$

函数的连续性

闭区间连续函数的零点定理

$f(x)$ 在闭区间 $[a,b]$ 上连续，不妨设 $f(a)<0,f(b)>0$

令 $E=\{x\big|f(x)\le 0,x\in[a,b]\}$

由于 $f(a)<0$ 可知 $E\ne\empty$。由 $f(b)>0$ 可知 $b$ 是 $E$ 的上界。

根据确界存在原理，可知 $E$ 的上确界 $\xi=\sup E\in[a,b]$ 存在

若 $f(\xi)<0$，则 $f(\xi)\in [a,b)$。

由连续函数的局部保号性知，$\exist\delta>0$，使 $\forall x\in(\xi-\delta,\xi+\delta)$ 时，都有 $f(x)<0$

此时有 $x_1\in(\xi,\xi+\delta)$ 使 $x_1\in E$ 且 $x_1>\xi$，这与 $\xi$ 是 $E$ 的上确界矛盾

若 $f(\xi)>0$，则 $f(\xi)\in(a,b]$

由连续函数的局部保号性知，$\exist\delta>0$，使 $\forall x\in(\xi-\delta,\xi+\delta)$ 时，都有 $f(x)>0$

此时有 $x_2\in(\xi-\delta,\xi)$ 使 $x_2$ 是 $E$ 的上界，这与 $\xi$ 是 $E$ 的上确界矛盾

由此可知，$f(\xi)=0$

闭区间连续函数的介值定理

$f(x)$ 在闭区间 $[a,b]$ 上连续，设 $f(a)=A$，$f(b)=B$，任取 $\min(A,B)<C<\max(A,B)$

构造函数 $\phi(x)=f(x)-C$，则 $\phi(a)=A-C$，$\phi(b)=B-C$

可见有 $\phi(a)$ 与 $\phi(b)$ 异号。

根据闭区间连续函数的零点定理，必有 $x_0\in(a,b)$ 使得 $\phi(x_0)=0$

此时 $f(x_0)-C=0$，$f(x_0)=C$

AM2 函数与极限

微分

费马引理

$\forall x\in u(x_0)$ 都有 $f(x)\le f(x_0)$

可见取 $x_0+\Delta x\in u(x_0)$ 都有 $f(x_0+\Delta x)\le f(x_0)$

则有 $f'_-(x_0)={\lim_{\Delta x\rarr 0^-}\\}\dfrac{f(x_0+\Delta x)-f(x_0)}{\Delta x}\ge 0$

以及 $f'_+(x_0)={\lim_{\Delta x\rarr 0^+}\\}\dfrac{f(x_0+\Delta x)-f(x_0)}{\Delta x}\le 0$

由于 $f(x)$ 在 $x_0$ 处导数存在，则其左右导数相等。

故 $0\le f'_-(x_0)=f'(x_0)=f'_+(x_0)\le 0$

有 $f'(x_0)=0$

洛必达法则

极限值与 $f(x)$ 和 $F(x)$ 在 $a$ 处的连续性无关。

为求解极限值，不妨假设其连续，即取 $f(a)=0$ 与 $F(a)=0$

此时根据柯西不等式任取 $x\ne a$ 有 $\dfrac{f'(x)}{F'(x)}=\dfrac{f(x)-f(a)}{F(x)-F(a)}=\dfrac{f(\xi)}{F(\xi)}$，其中 $\xi\in(a,x)$（或 $\xi\in(x,a)$）

令 $x\rarr a$，此时 $\xi\rarr x$，则有 ${\lim_{x\rarr a}\\}\dfrac{f'(x)}{F'(x)}={\lim_{x\rarr a}\\}\dfrac{f(\xi)}{F(\xi)}={\lim_{x\rarr a}\\}\dfrac{f(x)}{F(x)}$

函数的单调性

曲率公式1

曲率 $k=\begin{vmatrix}\dfrac{\Delta\alpha}{\Delta s}\end{vmatrix}$

对于曲线 $y=f(x)$，有 $y'=\tan\alpha$

两侧对 $x$ 求导有 $y''=\dfrac{1}{\cos^2\alpha}\dfrac{\Delta\alpha}{\Delta x}=(1+\tan^2\alpha)\dfrac{\Delta\alpha}{\Delta x}=[1+(y')^2]\dfrac{\Delta\alpha}{\Delta x}$

则 $\Delta\alpha=\dfrac{y''}{1+(y')^2}\Delta x$

由勾股定理，弧长 $\Delta s^2=\Delta x^2+\Delta y^2=\Delta x^2+(y'\Delta x)^2=[1+(y')^2]\Delta x^2$

故 $\Delta s=[1+(y')^2]^\frac{1}{2}\Delta x$

曲率 $k=\begin{vmatrix}\dfrac{\Delta\alpha}{\Delta s}\end{vmatrix}=\begin{vmatrix}\dfrac{\dfrac{y''}{1+(y')^2}\Delta x}{[1+(y')^2]^\frac{1}{2}\Delta x}\end{vmatrix}=\begin{vmatrix}\dfrac{y''}{[1+(y')^2]^\frac{3}{2}}\end{vmatrix}$

曲率公式2

曲率 $k=\begin{vmatrix}\dfrac{\Delta\alpha}{\Delta s}\end{vmatrix}$

对于曲线 $\begin{cases}y=y(t)\\x=x(t)\end{cases}$，有 $\tan\alpha(t)=\dfrac{y'}{x'}$。这里（下同）的 $x'$ 和 $y'$ 是 $x'(t)$ 和 $y'(t)$

则 $\alpha(t)=\arctan\dfrac{y'}{x'}$

则 $\alpha'(t)=\dfrac{1}{1+(\frac{y'}{x'})^2}\times\dfrac{y''x'-y'x''}{(x')^2}$

另外 $s'(t)=[(x')^2+(y')^2]^\frac{1}{2}$

则 $k=\begin{vmatrix}\dfrac{\Delta\alpha}{\Delta s}\end{vmatrix}=\begin{vmatrix}\dfrac{\alpha'(t)}{s'(t)}\end{vmatrix}=\begin{vmatrix}\dfrac{\dfrac{1}{1+(\frac{y'}{x'})^2}\times\dfrac{y''x'-y'x''}{(x')^2}}{[(x')^2+(y')^2]^\frac{1}{2}}\end{vmatrix}=\begin{vmatrix}\dfrac{y''x'-y'x''}{[(x')^2+(y')^2]^\frac{1}{2}}\end{vmatrix}$

AM3 积分

AM3.1 不定积分

第一类换元积分法 结论1

$\int\csc x\operatorname{dx}\\={\int\\}\dfrac{1}{\sin x}\operatorname{dx}\\={\int\\}\dfrac{1}{2\sin \frac{x}{2}\cos\frac{x}{2}}\operatorname{dx}\\={\int\\}\dfrac{\sec^2\frac{x}{2}}{2\tan\frac{x}{x}}\operatorname{dx}\\={\int\\}\dfrac{\operatorname{d\tan\frac{x}{2}}}{\tan\frac{x}2}\\=\ln\begin{vmatrix}\tan\frac{x}2\end{vmatrix}$

AM 3.3 反常积分

一阶线性微分方程的解

一阶线性微分方程为 $\dfrac{\operatorname{dy} }{\operatorname{dx} }+P(x)y=Q(x)$

设 $y=ue^{-\int P(x)\operatorname{dx}}$，其中 $u$ 是关于 $x$ 的函数。

代入原式，得到 $u'e^{-\int P(x)\operatorname{dx}}-ue^{-\int P(x)\operatorname{dx}}P(x)+P(x)ue^{-\int P(x)\operatorname{dx}}=Q(x)$

即 $u'e^{-\int P(x)\operatorname{dx}} = Q(x)$

则 $u'=Q(x)e^{\int P(x)\operatorname{dx}}$

得到 $u=\int Q(x)e^{\int P(x)\operatorname{dx}}\operatorname{dx} + c$

从而，$y=ue^{-\int P(x)\operatorname{dx}}=e^{-\int P(x)\operatorname{dx} }(\int Q(x)e^{\int P(x)\operatorname{dx}}\operatorname{dx}+c)$

AM4 向量代数与空间解析几何

AM4.1 平面

点到平面的距离公式

若平面的一般方程为 $Ax+By+Cz+D=0$，则其法线向量 $\overrightarrow{n}=(A,B,C)$

对于任意一点 $P_0=(x_0,y_0,z_0)$，记其与平面的距离为 $d$

从平面上任取一点 $P=(x,y,z)$，可见 $P$ 满足 $Ax+By+Cz+D=0$

做向量 $\overrightarrow{PP_0}=(x_0-x.y_0-y,z_0-z)$

向量 $\overrightarrow{PP_0}$ 与 $\overrightarrow{n}$ 的夹角 $\theta$ 有 $\cos\theta=\dfrac{d}{\begin{vmatrix}\overrightarrow{PP_0}\end{vmatrix}}$

则 $d=\begin{vmatrix}\overrightarrow{PP_0}\end{vmatrix}\cos\theta=\begin{vmatrix}\overrightarrow{PP_0}\end{vmatrix}\dfrac{\begin{vmatrix}\overrightarrow{PP_0}\bull\overrightarrow{n}\end{vmatrix}}{\begin{vmatrix}\overrightarrow{PP_0}\end{vmatrix}\begin{vmatrix}\overrightarrow{n}\end{vmatrix}}=\dfrac{\begin{vmatrix}\overrightarrow{PP_0}\bull\overrightarrow{n}\end{vmatrix}}{\begin{vmatrix}\overrightarrow{n}\end{vmatrix}}=\dfrac{A(x_0-x)+B(y_0-y)+C(z_0-z)}{\sqrt{A^2+B^2+C^2}}$

由于 $D=-Ax-By-Cz$，带入上式可得

$d=\dfrac{Ax_0+By_0+Cz_0+D}{\sqrt{A^2+B^2+C^2}}$

旋转曲面方程

假设母线为 $\Gamma:\begin{cases}F_1(x,y,z)=0\\F_2(x,y,z)=0\end{cases}$，旋转轴为直线 $l:\begin{cases}x=x_0+mt\\y=y_0+nt\\z=z_0+pt\end{cases}$

记旋转轴的方向向量为 $n=(m,n,p)$

从 $\Gamma$ 上任取一点 $K=(x_k,y_k,z_k)$，从 $l$ 上任取一点 $M=(x_0,y_0,z_0)$

则 $K$ 点所在纬圆上任意一点 $P=(x,y,z)$ 满足：

• $\overrightarrow{PK}\perp\overrightarrow{n}$
• $\begin{vmatrix}PM\end{vmatrix}=\begin{vmatrix}KM\end{vmatrix}$

即 $\begin{cases}m(x-x_k)+n(y-y_k)+p(z-z_k)=0\\(x-x_0)^2+(y-y_0)^2+(z-z_0)^2=(x_k-x_0)^2+(y_k-y_0)^2+(z_k-z_0)^2\end{cases}$

$K$ 是 $\Gamma$ 上一点，联立四式 $\begin{cases}m(x-x_k)+n(y-y_k)+p(z-z_k)=0\\(x-x_0)^2+(y-y_0)^2+(z-z_0)^2=(x_k-x_0)^2+(y_k-y_0)^2+(z_k-z_0)^2\\F_1(x_k,y_k,z_k)=0\\F_2(x_k,y_k,z_k)=0\end{cases}$

即可消去 $x_k,y_k,z_k$ 从而得到旋转曲面方程 $f(x,y,z)=0$

特殊情况的公式

当母线 $\Gamma$ 为 $yoz$ 平面上曲线，旋转轴为 $z$ 轴，此时有：

$\Gamma:\begin{cases}x=0\\F(x,y,z)=0\end{cases}$ 以及 $l:\begin{cases}x=0+0t\\y=0+0t\\z=z_0+pt\end{cases}$，其中 $p\not=0$

带入先前结论，有 $\begin{cases}p(z-z_k)=0\\x^2+y^2+(z-z_0)^2=y_k^2+(z_k-z_0)^2\\x_k=0\\F(x_k,y_k,z_k)=0\end{cases}$

前三个方程解得 $\begin{cases}z_k=z\\y_k=\pm\sqrt{x^2+y^2}\\x_k=0\end{cases}$

带入第四个方程 $F(x_k,y_k,z_k)=0$

即有 $F(\pm\sqrt{x^2+y^2},z)=0$

其余情况同理可证

AM5 多元函数

AM5.3 全微分

# 可微的必要条件

若 $z=f(x,\ y)$ 在点 $(x,\ y)$ 处可微

则 $\Delta z=f(x_0+\Delta x,\ y_0+\Delta y)-f(x_0,\ y_0)=\Delta z=A\Delta x+B\Delta y+o(\rho)$

令 $\Delta y=0$，则 $\Delta_xz=A\Delta x+o(\rho)$

有 $f'_x(x,y)={\lim_{x\rarr 0}\\}\dfrac{\Delta_xz}{\Delta x}={\lim_{x\rarr 0}\\}\dfrac{A\Delta x+o(\rho)}{\Delta x}=A$

同理可得 $f'_y(x,\ y)=B$

故 $\operatorname{dz}=A\Delta x+B\Delta y=f'_x(x,\ y)\Delta x+f'_y(x,\ y)\Delta y$

AM6 重积分

AM6.2 三重积分

# 三维空间曲面面积

对于三维空间曲面 $z=f(x,\ y)$，在曲面上任取一小面 $dA$，则其在 $xoy$ 平面上的投影为 $d\sigma$。

记 $dA$ 与 $d\sigma$ 的夹角为 $\theta$，可见 $dA=\dfrac{d\sigma}{\cos\theta}$

做 $dA$ 的法向量 $\overrightarrow{a}$ 与 $d\sigma$ 的法向量 $\overrightarrow{n}$，可见 $\overrightarrow{a}=(f'_x,\ f'_y,\ -1)$，$\overrightarrow{n}=(0,\ 0,\ 1)$

有 $\cos\theta=\dfrac{\left|\overrightarrow{a}\bull\overrightarrow{n}\right|}{\left|\overrightarrow{a}\right|\left|\overrightarrow{n}\right|}=\dfrac{1}{\sqrt{1+(f'_x)^2+(f'_y)^2}}$

则曲面面积为 ${\iint\limits_D\\}\dfrac{d\sigma}{\cos\theta}={\iint\limits_D\\}\sqrt{1+(f'_x)^2+(f'_y)^2}\ d\sigma$

AM7 无穷级数

AM7.2 交错级数

# 莱布尼茨定理

若交错级数 ${\sum\limits_{n=1}^\infin}(-1)^{n-1}u_n$ 满足 $u_n\ge u_{n+1}$ 且 $\lim\limits_{n\rarr\infin}u_n=0$

则 $S_{2n}=u_1-u_2+u_3-u_4+\ldots+u_{n-1}-u_n$

由于 $u_n\ge u_{n+1}$，可见 $S_{2(n+1)}-S_{2n}=u_{2n+1}-u_{2n+2}\ge 0$，即 $\{S_{2n}\}$ 非递减

又 $S_{2n}=u_1-(u_2-u_3)-(u_4-u_5)-\ldots-(u_{n-2}-u_{n-1})-u_n$

可见 $S_{2n}\le u_1$，即 $\{S_{2n}\}$ 有界。记 $\lim\limits_{n\rarr\infin}S_{2n}=S$

又因 $\lim\limits_{n\rarr\infin}S_{2n+1}=\lim\limits_{n\rarr\infin}S_{2n}+u_{2n+1}=S$

则 $\lim\limits_{n\rarr\infin}S_n=S$，即交错级数 ${\sum\limits_{n=1}^\infin}(-1)^{n-1}u_n$ 收敛

AM7.3 任意项级数

# 任意项级数定理

若绝对值级数 ${\sum\limits_{n=1}^\infin}\left|u_n\right|$ 收敛

记 $v_n=\dfrac12(u_n+\left| u_n\right|)$，有 $0\le v_n\le u_n$

此时 ${\sum\limits_{n=1}^\infin}v_n$ 收敛。由于 ${\sum\limits_{n=1}^\infin}u_n={\sum\limits_{n=1}^\infin}2v_n-\left| u_n\right|$，故而任意项级数 ${\sum\limits_{n=1}^\infin}u_n$ 收敛